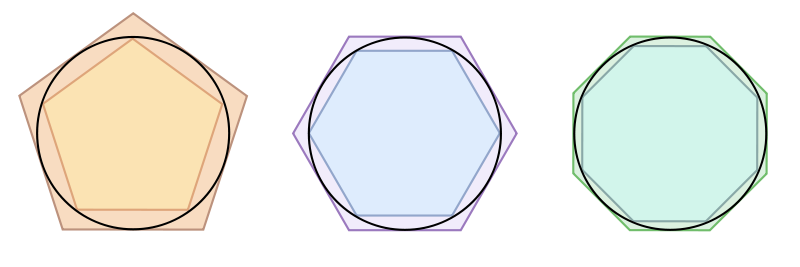
紀元前3世紀、古代ギリシャにて多数の科学的証明、発明を行った 天才科学者・アルキメデス。 現代でも馴染み深いものを挙げると円周率やてこの原理も、彼が証明したものです。 証明した理論にはあまりにも有名なものが名を連ねていますし、何よりすごいのは、今から00年以上も前アルキメデス の手法を極端 「 3 14 」 ならぬ 「 3 」 で扱っていい円周率 。 日常生活では大体それでいいけれど・・・ 最近ではまた 3.14 にもどったようだ。 計算で円周率に近い数を求めるんだよ。僕たちはいま、円周率が入っている範囲を求めようとしている。アルキメデスの方法ではこんな不等式を使う」 $$ \text{内接正 $n$ 角形のまわりの長さ(赤)} \text{円周} \text{外接正 $n$ 角形のまわりの長さ(青)} $$
粉体技術用語 一般社団法人日本粉体工業技術協会
アルキメデス 円周率 発見
アルキメデス 円周率 発見-ここでは、円周率に関わった有名人をご紹介します。 ① アルキメデス(古代ギリシャ) 紀元前3世紀、円の面積の公式を証明。 ② 祖沖之(中国) 5世紀、円周率を7桁まで求める。この記録は、約1000年間塗り替えられなかった。円周率の計算 作成者 Bunryu Kamimura アルキメデスは正96角形を描いて円周率を求めた。 下のやり方だと、正多角形は4の倍数になり、32角形→64角形→128角形になる。 とすると、アルキメデスは正3角形から出発し、3→6→12→24→48→96角形と計算したことが



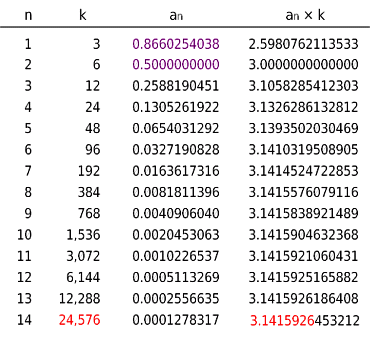
円周率に収束する数列
たところ,円周が271mm, 直径がmmとなった.円周÷直径は271= = 304 である.円周率の計算について,歴史的にどのような工夫がなされてきたか,ア ルキメデス,和算家,インド,ガウスの方法を紹介し,彼らの計算を追体験する ことによって,人類の知的活動の歴史を鑑賞してみよう. 1 円の面積による計算となるので,円周率が 305 305 305 より大きいことが証明された。 定番の手法で知っている人も多いでしょう。 試験上では計算機が使えないのでルートの大雑把な評価が求められます。 この解法では, 4 2 − 2 > 305 4\sqrt {2\sqrt {2}} > 305 4 2− 2ホーム / 技術開発(r&dディスクロージャ) / 基本物理定数と単位換算 / 円周率(pi) 100万(1,000,000)桁 円周率(PI) 100万(1,000,000)桁 10億桁はこちら(ダウンロードZIP,447MB)
アルキメデスの円周率の求め方 アルキメデスは,円に正多角形を内接,または外接させると,次の 不等式が成り立つことを利用して,円周率を計算しました。 このとき円の直径を 1 とすると,円周の長さ = 1 ×π =π となる ので, 円周 = 円周率π と考えることができます。ここでは歴史的な円周率の求め方を振り返りながら,面倒な数 値の計算はパソコンの表計算ソフト(エクセル)を用いて実際に 計算して見よう. 円周率は「円周の長さと直径の比」ということはいいですね. 目次 1.アルキメデスの方法コラム 円周率(難易度1) どのような半径の円もすべて相似で、「円周の長さ÷直径の長さ」はすべて同じ数値になります。 この数値が円周率で、πと呼ばれます。 円の面積の計算にもこの定数が登場しますが、分数でも平方根のような根号でも書き表せ
アルキメデスは幾何学よりも計算の方に興味をもった。その一つの例として、円周率の計算がある。 彼は『円と計測』という著書の中で、円周率が3 (3142)より小さく、3 (3140)より大きいことを理論的に証明している。 1386 スp ス スレ撰ソス スU スp ス` スフ外 ス ス 1 スp ス ス 186 スp スO スレ撰ソス スP スQ スp ス` スフ外 ス ス スp円周率の計算 円周率はπという記号で表現しますが、 π=・・・ と無限に続き、分数のように循環もしません。 このような数を無理数と呼んでいます。




インディアナ州円周率法案 Wikipedia




コンプリート 円周率 3 円周率 31兆桁
法 値 アルキメデス は、円の面積が円周率と半径の平方の積に等しいことを証明した 。アルキメデスによる円周率の計算(平成12年) 1 はじめに アルキメデスは紀元前0年頃に活躍した大天才である 彼が求めた円周率 は小数第2位,314まで正しく計算されていた 彼の死後,1,400年もの間,こ れを凌ぐ円周率が出現することはなかった算術幾何平均と円周率 上越教育大学 中川仁 平成21年9月18日 1 アルキメデスの方法による円周率の計算 定義11 正の実数a,bに対して, A(a,b) = ab 2, G(a,b) = p ab, H(a,b) = 2ab ab = A(a−1,b −1) とおく.A(a,b)を算術平均, G(a,b)を幾何平均,H(a,b)を調和平均という.



腕試し問題 解析の問題 江戸の数学



3はドコまで円周率か 円周率を3と教えることの是非
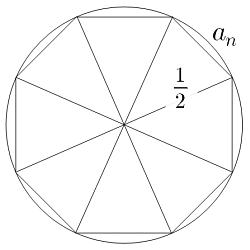
π~円周率の神秘~ 研究者 青木活人 Ê林純也 齊藤啓太 中畑未来 古畑菜々子 指者 倉田慎司先生 1 研究の動機 私たちの身の回りに無数に存在している円だが、その円周率の値はどこまでも続いてい くような値になる、と一般的に知られている。円周率小史―アルキメデス前後について― (平成13年) 1 はじめに アルキメデスが計算した円周率は, 円に内外接する正多角形の周の長さを求めること で計算された(アルキメデスによる円周率の計算Bn1 = q an1bn とすれば、an、bn はそれぞれ直径1の円に外接、内接する正6¢2n 角形の長さになり ます。




The Strange Storage Coneとcylinder




入試伝説 13年 大阪大学 先人達が歩んだ円周率の歴史を辿る ルドルフの偉業 受験の月
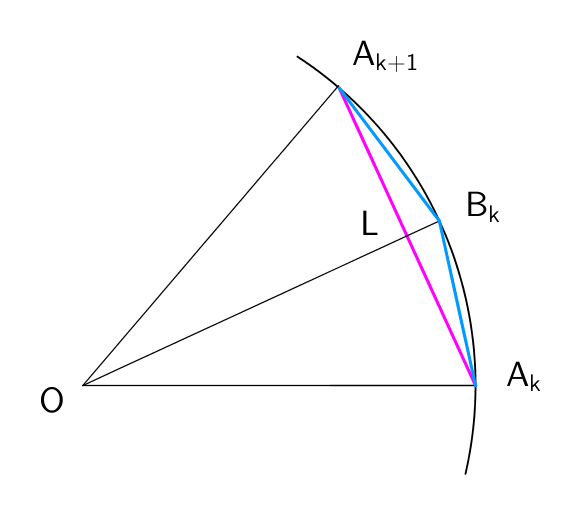
2 円周率計算の基本となる公式 21 正多角形による方法 円周率の古くからの計算法は正多角形で円を近似する方法です。a0 = 2 p 3, b0 = 3 として an1 = 2anbn an bn;< ˇ(= 円周率) < 3 1 7 を示したのはアルキメデスである 標語的には「哲学的・理学的なユークリッド, 算数的・工学的なアルキメデス」となる 世界三 大数学者と言えば, 「アルキメデス, ニュートン, ガウス」が定説(俗説?) であり, アルキメデス 21年7月2日放送のNHK「チコちゃんに叱られる!」で出題されたのは『円周率がずっと続くのはなぜ?』という問題。そもそも円周率を分かりやすく説明すると一体何なのでしょうか?そして円周率が限りなくずっと続く理由とは? AdSense ゲスト出演者 ゲスト野々村真、堀田茜



フナハシ学習塾数学18 P円周率のはなし




円周率 英語 説明
(数と科学のストーリー)円周率 アルキメデスは考えた 3.。 これは、惑星探査機「はやぶさ」にプログラムされた16桁の円周率です。 その円周の長さから円周率を求めるのがアルキメデスの方法です。 この図による説明と、実際に円周を計測する方法を組み合わせてみると、かなり理解が深まるでしょう。 まとめ 円周率の求め方というのは、大人からしてもなかなか難しい問題です。この功績のなかに円周率がある。円周率の歴 史のなかで最も有名な人物が、アルキメデス である。アルキメデスは次のように円周率を 求めた。 まず、円の内側と外側に接する正多角形を 描いた。円の周の長さは内接する正多角形の 周の長さより長い。



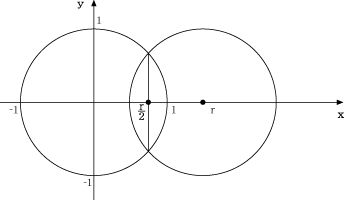
Rの値




小学校算数 5学年 Wikibooks
アルキメデスに倣って円周率を計算する 円周に長さがあるということは直観的に誰でも知っていることであり 円周の長さ 円の直径 が円の大きさによらない定数であることも四千年前から知られていたようである この定数 を円周率とよび通常 で表わす■円周率近似値の日とは 紀元前3世紀、「7分の22」が円周率の大きめの近似値であることを、古代ギリシアの第一級科学者アルキメデスが証明したことから、 7月22日が円周率近似値の日 となりまし3 アルキメデスによる円周率の求め方 アルキメデスは,円に内接する多角形と円に外接する多角形の周の長さを求めることによ り,円周率を計算しました.まずは彼の著書「円の測定について」により,その方法を再 現してみることにしましょう.




アルキメデス Wikiwand




コンプリート 円周率 3 円周率 31兆桁




数学で最も美しい定理 オイラーの等式




ピラミッド計算その4 Sakurai Susumu Website



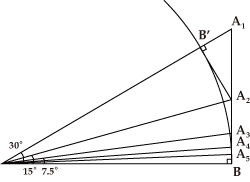
腕試し問題 解析の問題 解答 江戸の数学



アルキメデス Wikiwand



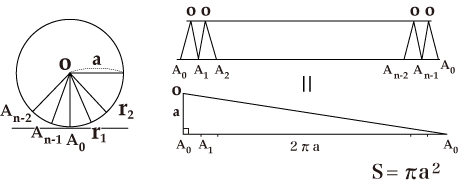
円の面積




アルキメデスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com



腕試し問題 解析の問題 江戸の数学



Pの桁数の伸び
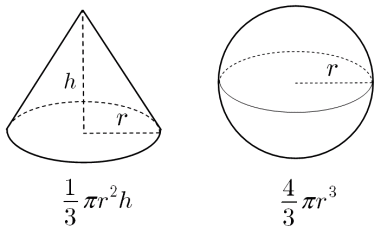



積分 円の面積の再考 大人が学び直す数学



東大入試問題 円周率が3 05より大きいことを証明せよ



アルキメデスの失われた本 Mysterious Questions In The World



円周率に収束する数列



粉体技術用語 一般社団法人日本粉体工業技術協会



東大入試問題 円周率が3 05より大きいことを証明せよ
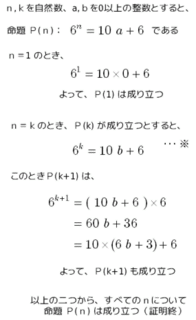



数列 円周率を数列で求める 大人が学び直す数学
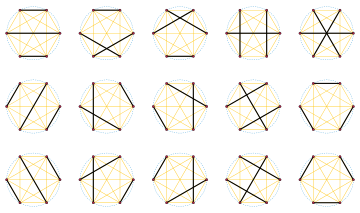



新着記事一覧 隠れ家 楽天ブログ




取り尽くし法 取り尽くし法の概要 Weblio辞書
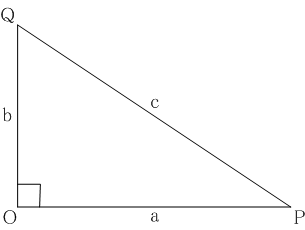



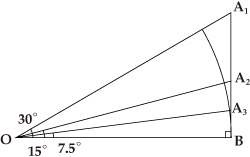
1 10節 角度論



新着記事一覧 隠れ家 楽天ブログ



大学入試問題001
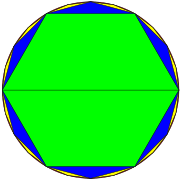



円周率 Wikipedia



3はドコまで円周率か 円周率を3と教えることの是非




円周率 Wikiwand




チコちゃんに叱られる ドンヨリ空と憂うつ 男爵いも秘話 円周率の謎 字 の番組内容解析まとめ チコちゃんに叱られる
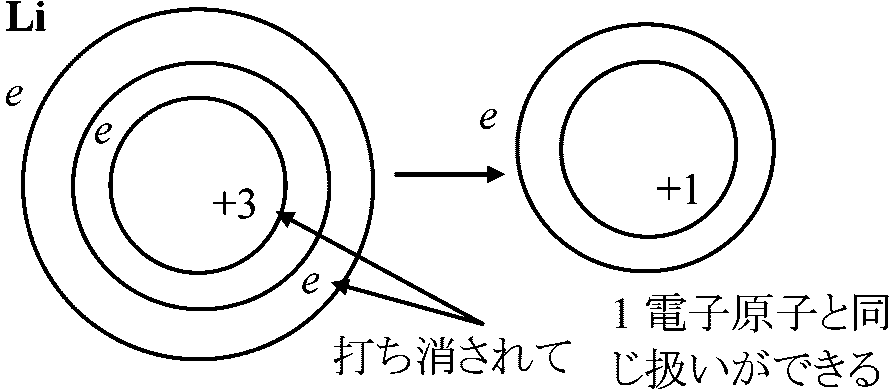



自然科学概論
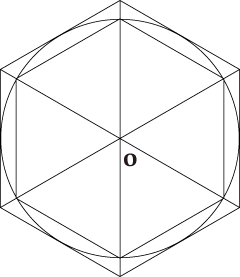



腕試し問題 解析の問題 江戸の数学




Images Of 円周率の歴史 Japaneseclass Jp
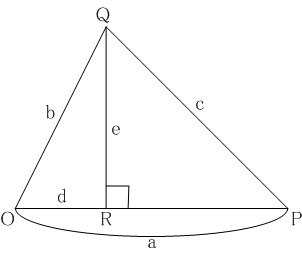



1 10節 角度論




アルキメデスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com



東大入試問題 円周率が3 05より大きいことを証明せよ
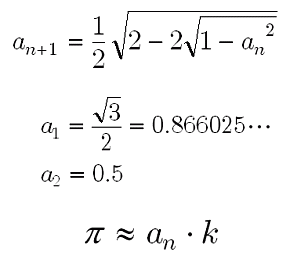



数列 円周率を数列で求める 大人が学び直す数学




Manukeno Blog Tumblr Blog Tumgir



疑似歴史学事典 ピラミッドと円周率p
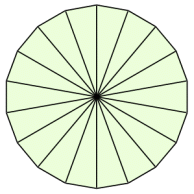



積分 円の面積の再考 大人が学び直す数学



3はドコまで円周率か 円周率を3と教えることの是非




円周率 Wikipedia




円周率 Wikiwand



円周率の求め方 過去のブログ



数列 円周率を数列で求める 大人が学び直す数学



My Math Note



大学入試問題001



Q Tbn And9gcrkcmytr4gb5xhrvk2qmkre V29ujpkf14h3wb8tk1aoyu7r1o1 Usqp Cau




円周率 Wikiwand



東大入試問題 円周率が3 05より大きいことを証明せよ



3はドコまで円周率か 円周率を3と教えることの是非




数学って暗記 Vipper銀河系




小学校算数 5学年 Wikibooks




円周率算出の一方法 ものづくり筆耕



Rの値




解法のテクニック センターラインの公式




読書ノート 武藤 徹著 面積の発見 岩波科学ライブラリー 12年 ブログ ごまめの歯軋り



Fortranは今でも数値計算で使われているのでしょうか Quora



東大入試問題 円周率が3 05より大きいことを証明せよ



2



おもしろ教科 数学 の世界



数学iii 式と曲線 のコンピュータ利用にsnap Byob 4 0 を用いる



フナハシ学習塾数学18 P円周率のはなし



アルキメデスの生涯と功績 残した名言 格言 ビジネス知恵袋




アルキメデスが残した発見した原理のまとめ なんで水に物が浮くのか



3はドコまで円周率か 円周率を3と教えることの是非




アルキメデスとはどんな人物 簡単に説明 完全版まとめ 歴史上の人物 Com



円周率に収束する数列



腕試し問題 解析の問題 解答 江戸の数学




ファイル Archimedes Pi Svg Wikipedia



数列 円周率を数列で求める 大人が学び直す数学



アルキメデスの生涯と功績 残した名言 格言 ビジネス知恵袋



中学受験ー算数解き方ポータル 14年11月



円の面積




算数 5年生 正多角形と円 円周率 授業力アップ 学級経営の話



円周率に収束する数列



3月14日今日は何の日 円周率の日 なぐブロ




円周の測定 Measurement Of A Circle Japaneseclass Jp




コンプリート 円周率 3 円周率 31兆桁




一行数学史




外接の新着記事 アメーバブログ アメブロ



ファイル Archimedes Pi Svg Wikipedia




アルキメデス Wikipedia




The Strange Storage Coneとcylinder



算数オリンピック 中学受験ー算数解き方ポータル




円周率が 3 だったら どうなる 計算問題 Com 脳トレ 就活に




鐶 中古枕木 玄関先の据物 造園 お庭造り まくらぎ 編格枕木 国産枕木 1本サイズ 削減枕木 貨物輸送積書き 人間住み処は送りとどける不実行可能 Acilemat Com




Pi Pi Wikipedia



円周率の歴史 紀元前00年頃 1706年 ユウの気まぐれブログ




Pi P に隠された美女たち




無理数 Wikipedia




Jiavkfbsdrvaem



円周率に収束する数列




円周率pの不思議 アルキメデスからコンピュータまでの通販 堀場 芳数 ブルー バックス 紙の本 Honto本の通販ストア




鐶 中古枕木 玄関先の据物 造園 お庭造り まくらぎ 編格枕木 国産枕木 1本サイズ 削減枕木 貨物輸送積書き 人間住み処は送りとどける不実行可能 Acilemat Com


0 件のコメント:
コメントを投稿